
수학 이야기...숫자
효율성이 높은 에너지가 선택되는 것은 자연의 근본원리에 따른 결과이기도 합니다.
빛은 항상 시간이 가장 적게 걸리는 경로로 이동합니다. 이를 페르마의 원리(Fermat's principle)라고 하는데,
이렇듯 자연은 효율성을 추구합니다. 수학도 마찬가지입니다.
만일 숫자 '0'이 없다면 우리는10, 20, 30, 및 10,000과 같은 숫자를 어떻게 표시했을까요?
만일 '0"이 없었다면 이를 표현하기 위해서는 또다른 숫자를 만들었어야 했을 겁니다다.
숫자 ' 0'이 지닌 효율성은 엄청납니다.
자연을 탐구하는데 쓰이는 수학은 당연히 자연의 원리를 따르며, 효율성을 추구합니다.
# 우리가 쓰는 숫자와 기호 이야기
우리가 사용하고 있는 숫자 1, 2, 3, 4, 5... 를 보통 아라비아 숫자라고 하지만 원래는 인도
사람에게서 나온 것으로 1, 2, 3, 4, 5 ... 하고 나가다가 끝에 "0" 이 생긴 것도 사실은
1400-1500년경 인도에서 발명되었다.
옛날 아라비아 상인들이 실크 로드를 통해 무역을 하면서 9 세기경 인도를 방문했을 때
인도인들이 "0" 의 개념을 사용하는 것을 보고는 그 편리함에 매혹되어 점차 유럽에
"0" 의 개념을 알리게 되었는데 처음 유럽인들은 자존심을 내세우느라 쓰지않고 일부러
외면했다가 1800년 경에야 마지못해 "0" 이라는 숫자를 쓰게 되었다.
" 0 " 이 있기 전에는 숫자 "102" 를 1 과 2 사이에 "0" 대신 그냥 한 칸을 비워놓아
" 1 2 " 라고 표시하여 당시 많은 혼란과 불편이 있었고 심지어는 이집트 조차도 "0"
이란 표기가 없어 ". " 과 같이 점을 사용하여 "102" 를 "1 . 2" 로 표시했었는데
인도인들의 "0" 표시의 발명으로 전세계가 "0" 을 쓰게된 것이다.
그 당시 유럽은 로마인들이 사용하던 I, II, III, IV, V .... 즉 " 로만 표기법" 을 고수했지만
큰 숫자로 갈수록 복잡해져 하는 수없이 1, 2, 3, 4, 5 ... 0 이란 숫자를 사용하게 된
것이다. 따라서 1, 2, 3, 4, 5 ..... 0 은 아라비아 숫자가 아니고 정확히 말하면 " 인도
숫자 " 인 셈이다.
또한 우리가 흔히 쓰고 있는 기호 " + " , " - " , " x ", " ÷ " 가 발명되기 전까지는 일일이
이런 개념을 문장으로 써야 했는데 예를 들면 "1+1=2 " 는 " 1 더하기1은 합해서 2 "라고
썼다. 덧셈과 뺄셈 기호 " + " 와 " - " 는 1489년에 독일의 비드만(Widman) 이라는
회계사가 그의 나이 29세에 처음 만들어 냈고
곱셈 기호 "x" 는 1631년 영국의 수학자 윌리암 오트레드(William Oughtred) 가 발명
했으며 나누기 기호 "÷" 는 1659년 스위스의 기호학 연구가인 "요한 하인리히 라안 "
이 만들어 냈다.
그리고 "도합 또는 합" 이라는 기호 "=" 는 1557년 영국의 수학자요 의사인 로버트
레코드(Robert Recorde) 가 그의 저서" 기지(機智)의 숫돌" 이라는 영국 최초의
대수서(代 數 書) 에서 처음으로 썼다.
그는 기차의 레일을 보고 아이디어를 얻었는데 세상 어느 것도 평행선 같이 끝까지
갈 수는 없고 언젠가는 합쳐져야 하지 않겠는가 하며 "합" 이라는 기호 "=" 을 발명
했다.
기호 "<" 와 ">" 는 1661년 영국 최초의 대수학자 토마스 해리엇(Thomas Harriot) 이
음악에서 쓰는 " 점점 크게 " 또는 " 점점 작게 " 에서 고안했고 괄호를 뜻하는 "( )"의
기호는 1556년 이태리의 수학자요 물리학자인 니콜로 타르탈리아 ( Niccolo
Tartaglia ) 가 발명했다.
& 우리가 가끔"천재 일우"의 기회라는 말을 사용하는데,이 말뜻을 아시나요?천재(千載) 에서 1載=10,000,000,000,000,000,000,000,000,000,000,000,000,0000,000 (10의 44승) 이라는 뜻입니다.
그러므로 천재(千載) 10의 47승 (10의 12승이 조이므로 어마어마 하죠) 의 확률로 생긴 기회란 뜻입니다.
보통 집값을 얘기할 때, 억 단위를 사용하고, 나라 예산을 얘기할 때는 조를 사용하는데,
수의 단위에 대해 알아 보면 아래와 같습니다. (** 는 몇 승을 의미합니다.)
| 일 |
一 |
10**0 |
| 십 |
拾 |
10**1 |
| 백 |
百 |
10**2 |
| 천 |
千 |
10**3 |
| 만 |
萬 |
10**4 |
| 억 |
億 |
10**8 |
| 조 |
兆 |
10**12 |
| 경 |
京 |
10**16 |
| 해 |
垓 |
10**20 |
| 시 |
|
10**24 |
| 양 |
穰 |
10**28 |
| 구 |
|
10**32 |
| 간 |
澗 |
10**36 |
| 정 |
正 |
10**40 |
| 재 |
載 |
10**44 |
| 극 |
極 |
10**48 |
| 향하사 |
恒河沙 |
10**52 |
| 아승지 |
阿僧紙 |
10**56 |
| 나유타 |
那由他 |
10**60 |
| 불가사의 |
不可思議 |
10**64 |
| 무량대수 |
無量大數 |
10**68 |
어마어마 하죠? 이렇게 큰 수를 쓸 일도 없는데 만들어 낸 것이 신기합니다.
이것 외에도 큰 숫자는 아래와 같습니다.
겁(劫) : 한 세상이 창조되어 말세 후 다시 창조 될 때까지의 시간
사방 사십 리 되는 바위를 백 년에 한 번씩 천사가 입은 비단옷이 스쳐서 다 닳는 세월
작은 수를 알아 볼까요?
| 1) 먼지를 말하는 진 (塵) |
10**(-9) |
| 2) 모호한 상태 |
10**(-13) |
| 3) 순식간 |
10**(-16) |
| 4) 찰나 |
10**(-18) |
| 5) 청정(淸淨) |
10**(-21) |
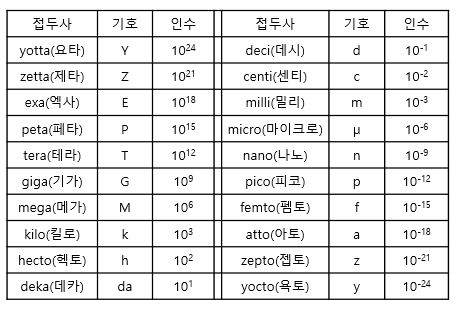
서양에서 사용하는 단위는 아래와 같습니다. (손으로 적기 힘들어서, 복사해 왔어요. ^^)
컴퓨터에서 저장용량을 표시할 때는, M, G, T 를 많이 쓰고 (큰 숫자이므로)
반도체 개발할 때는 회로폭 작은 것은 얘기하므로 n, p를 사용합니다.
사용하는 원칙은 큰 숫자는 대문자로, 작은 숫자는 소문자로 표현합니다.
|